Módulo e Argumento
Representando esse número complexo no plano de Argand-Gauss, teremos:
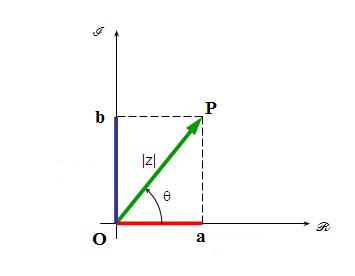 O segmento de reta OP é chamado de módulo do número complexo. O arco formado entre o eixo horizontal positivo e o segmento OP, no sentido anti-horário, é chamado de argumento de z. Observe a figura abaixo para determinarmos as características do argumento de z.
O segmento de reta OP é chamado de módulo do número complexo. O arco formado entre o eixo horizontal positivo e o segmento OP, no sentido anti-horário, é chamado de argumento de z. Observe a figura abaixo para determinarmos as características do argumento de z.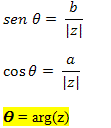
Podemos constatar, também, que:

Ou
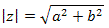 Exemplo 1. Dado o número complexo z = 2 + 2i, determine o módulo e o argumento de z. Solução: Pelo número complexo z = 2 + 2i, sabemos que a = 2 e b = 2. Segue que:
Exemplo 1. Dado o número complexo z = 2 + 2i, determine o módulo e o argumento de z. Solução: Pelo número complexo z = 2 + 2i, sabemos que a = 2 e b = 2. Segue que:
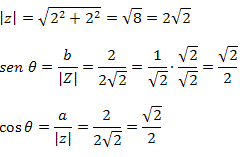
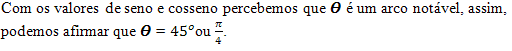

Ou
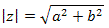 Exemplo 1. Dado o número complexo z = 2 + 2i, determine o módulo e o argumento de z. Solução: Pelo número complexo z = 2 + 2i, sabemos que a = 2 e b = 2. Segue que:
Exemplo 1. Dado o número complexo z = 2 + 2i, determine o módulo e o argumento de z. Solução: Pelo número complexo z = 2 + 2i, sabemos que a = 2 e b = 2. Segue que: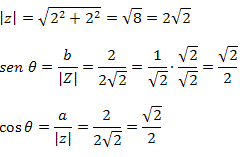
Forma Trigonométrica de um Número Complexo Sabemos que um número complexo possui forma geométrica igual a z = a + bi, onde a recebe a denominação de parte real e b parte imaginária de z. Por exemplo, para o número complexo z = 3 + 5i, temos a = 3 e b = 5 ou Re(z) = 3 e Im(z) = 5. Os números complexos também possuem uma forma trigonométrica ou polar, que será demonstrada com base no argumento de z (para z ≠ 0).
Considere o número complexo z = a + bi, em que z ≠ 0, dessa forma temos que:cosӨ = a/p e senӨ = b/p. Essa relações podem ser escritas de outra forma, acompanhe:
cosӨ = a/p → a = p*cosӨ
senӨ = b/p → b = p*senӨ
Vamos substituir os valores de a e b no complexo z = a + bi.
z = p*cosӨ + p*senӨi → z = p*( cosӨ + i*senӨ) Essa forma trigonométrica é de grande utilidade nos cálculos envolvendo potenciações e radiciações. Exemplo 1 Represente o número complexo z = 1 + i na forma trigonométrica. Resolução: Temos que a = 1 e b = 1
.jpg) A forma trigonométrica do complexo z = 1 + i é z = √2*(cos45º + sen45º * i).
A forma trigonométrica do complexo z = 1 + i é z = √2*(cos45º + sen45º * i). Exemplo 2 Represente trigonometricamente o complexo z = –√3 + i.
Resolução:
a = –√3 e b = 1
.jpg) A forma trigonométrica do complexo z = –√3 + i é z = 2*(cos150º + sen150º * i).
A forma trigonométrica do complexo z = –√3 + i é z = 2*(cos150º + sen150º * i).
Nenhum comentário:
Postar um comentário