POEMAS E POESIA
Leia aqui alguns poemas e poesia relacionados aos números complexos e algo a mais sobre matemática:
Romance Matemático
abril 4, 2010 às 8:46 pm
Dê-me o silêncio…
Para eu dizer que nosso romance é como uma equação
Em que ponho-me, insistentemente;
A descobrir o valor de sua incógnita.
Dê-me o silêncio…
Para eu derrubar todos os axiomas;
Que insistem em dizer que nosso amor é impossível.
Dê-me o silêncio…
Para eu dizer que você é o pivô de minha matriz escalonada;
Que cada virtude que encontro em você
É um determinante para nossa relação.
Dê-me o silêncio…
Para eu dizer que a função que rege minha vida
Consiste em que cada elemento do seu domínio
Está associado a um elemento de meu contra-domínio.
Dê-me o silêncio…
Para eu te mostrar que nossas retas paralelas se encontrarão no infinito.
Dê-me o silêncio…
Para eu dizer que quando contemplo a imagem de seu corpo,
Meus batimentos cardíacos modelam uma cossenóide.
Dê-me o silêncio…
Para te provar que embora sejamos ângulos opostos pelo vértice,
nossas medidas são iguais.
Nesse instante me calo e quem diz tudo é você.
Andreson Costa dos Santos Souza e Alex Bruno Carvalho dos
Santos
O Quociente
abril 4, 2010 às 8:47 pm
O quociente perguntou à secante:
- Posso ser seu amante?
Ela, de pronto, respondeu:
- Nunca! Já tenho um amor,
- É o terno denominador…
Logo, então, se sentiu um resto.
Não era mais um número inteiro…
Passou, então, por perto a tangente,
Que caminhava para o infinito
Para se encontrar sabe lá com quem.
Perguntou aflito:
- Onde poso encontrar as paralelas?
Ela, então, respondeu:
- Talvez nunca.
Surgiu, então, do menos infinito, a esfera.
Bela e radiosa, logo esqueceu a secante.
Calculou seu manequim,
Mas se achou muito pequeno para tanto volume…
O quociente ficou triste,
Transformou-se em um número complexo
E numa relação unívoca,
Partiu para o esquecimento,
Tornando-se um ângulo obtuso.
André M. Hemerly
Amormetria
abril 4, 2010 às 8:58 pm
(Autor Desconhecido)
Dê-me um apoio (centro)
Num piscar de olhos me transformo em um compasso
Giro 90º, 180º, 270º, 360º graus
Volta completa na circunferência chamada vida.
Dê-me uma régua ou uma trena
Com ela conseguirei medir ou não nossa distância
Que parece infinita.
Dê-me um transferidor para medirmos os graus do nosso amor.
Um esquadro
Quem sabe ele possa nos enquadrar.
Dê-me um ponto
Por ele passarei infinitos segmentos de sentimentos
Paixão, amor, raiva, ressentimento, gratidão…
Só não me limite com dois pontos
Pois, não saberia que segmento de sentimento
Passaria por eles.
Edi Santana Barbosa
Professor da rede Estadual e municipal de Juazeiro BA
Pós-graduado em Metodologia e Didática do Ensino Superior.
Equacionando o amor
|
|
|
Considerando a seguinte afirmação:
O amor é o produto de um homem com uma mulher.
Chamando eu (o homem) de a e você (a mulher) de b,
temos:
amor = a*b
Agora, se somarmos a segunda potência do homem com a
segunda potência da mulher e o amor de cada um formaremos o trinômio quadrado
perfeito:
a*a + 2*a*b + b*b
Porém, se extrairmos a raiz quadrada dessa equação irá
sobrar apenas eu e você, ou seja, irá sobra a+b, pois (a+b)*(a+b) =
a*a + 2*a*b + b*b.
Agora eu pergunto: Cadê o amor? Será que ele não existe? A
resposta é essa: O amor existe, mas não podemos vê-lo porque está em nossos
corações. Amo-te muito, mesmo que você não perceba, não quer dizer que este
amor não exista.
Renato Bezerra Kato.
|
Aula de Matemática
|
|
|
|
Pra que dividir sem raciocinar
Na vida é sempre bom multiplicar
E por A mais B
Eu quero demonstrar
Que gosto imensamente de você
Por uma fração infinitesimal,
Você criou um caso de cálculo integral
E para resolver este problema
Eu tenho um teorema banal
Quando dois meios se encontram desaparece a fração
E se achamos a unidade
Está resolvida a questão
Prá finalizar, vamos recordar
Que menos por menos dá mais amor
Se vão as paralelas
Ao infinito se encontrar
Por que demoram tanto os corações a se integrar?
Se infinitamente, incomensuravelmente,
Eu estou perdidamente apaixonado por você.
Antônio Carlos Jobim
|











 a = c e b = d
a = c e b = d.jpg)
.jpg)
.jpg)
.jpg)
.jpg) .
.




 é descrito como tendo uma componente real a e uma componente imaginária b, que podem ser representadas por:
é descrito como tendo uma componente real a e uma componente imaginária b, que podem ser representadas por:



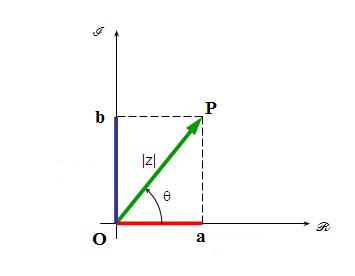
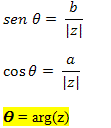

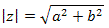
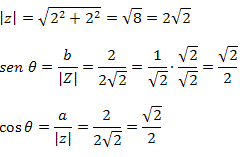
.jpg)
.jpg)

 que pode ser escrito na forma
que pode ser escrito na forma 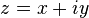 , em que
, em que  e
e  são números reais e
são números reais e  denota a unidade imaginária. Esta tem a propriedade
denota a unidade imaginária. Esta tem a propriedade  , sendo que
, sendo que  , contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de mesma denominação nos números reais, adquire uma estrutura algébrica denominada corpo algebricamente fechado, sendo que esse fechamento consiste na propriedade que tem o conjunto de possuir todas as soluções de qualquer equação polinomial com coeficientes naquele mesmo conjunto (no caso, o conjunto dos complexos). O conjunto dos números complexos também pode ser entendido por seu isomorfismo com um espaço vetorial sobre
, contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de mesma denominação nos números reais, adquire uma estrutura algébrica denominada corpo algebricamente fechado, sendo que esse fechamento consiste na propriedade que tem o conjunto de possuir todas as soluções de qualquer equação polinomial com coeficientes naquele mesmo conjunto (no caso, o conjunto dos complexos). O conjunto dos números complexos também pode ser entendido por seu isomorfismo com um espaço vetorial sobre  , o conjunto dos reais.
, o conjunto dos reais. .
.






